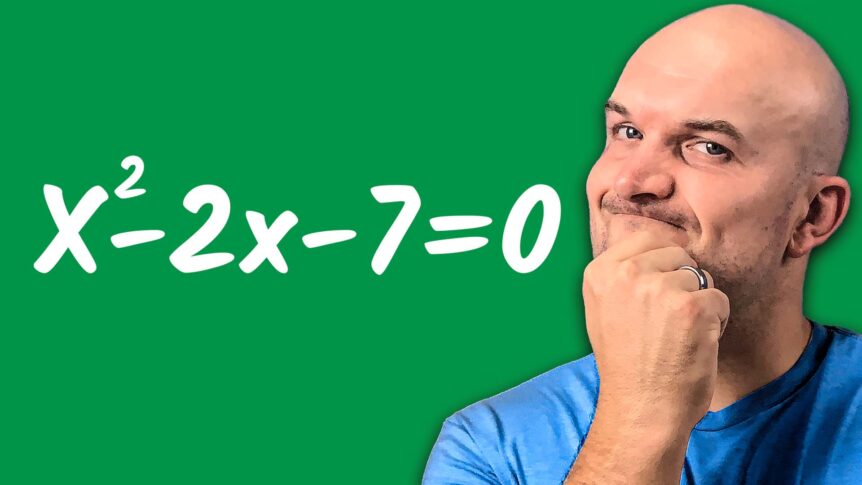Is it possible that factoring will fail us? That’s correct we need completing the square. Look at this problem: X squared minus two, X minus seven are factorable but not factorable across rational numbers. It will actually be multiplied by irrational numbers. Now, I believe it is critical to ensure that you understand how to factor. But what if a problem cannot be factored across rational numbers? It can become quite difficult. So, in this video, I’d like to inform you that there is no way to solve the quadratic as well as rewrite it in factor form which is by completing the square. But there is one thing I do not want you to do: make these two errors.
Mistake #1
The first error is to simply add out the seventh on both sides and then say Ax squared minus two X equals a seven. There aren’t many students here, so they must be thinking about something. So they’ll subtract the X and get an X minus two equals seven. And then, instead of using the zero product property, they simply say, “Well, why don’t we use the seven product property?” I’m not sure what you’d call it or what you’d do, but you can’t do this. Okay, so we use the zero product property when our product is equal to zero and not any other number. As a result, this does not work.
Mistake #2
Another mistake I see students make is, similar to the inverse operations, they want to isolate the term when we have an X squared minus two X minus seven. So they add a two X to both sides and a seven to both sides, resulting in an X squared equal to a two X plus seven. Now they say, well, I can just take the square root of both sides to solve for X. As a result, X is equal to a plus or minus the square root of two X plus seven. But keep in mind that when you learn that the vocabulary cannot be in the definition, we can’t solve for X if X is part of the decision. That doesn’t really tell us anything about the solution. Please, if you have a quadratic, do not do this as well. So we can’t factor when factoring fails. We do not want to make these two errors. What are our options?
Previous Video
In my previous video, we discussed the simplest way to solve quadratic equations. And the simplest way to solve quadratics was not to use inverse operations like this. We can’t use inverse operations in this case, but we can use them when we only have one variable. Remember, this was a simple problem with only one variable. So all we needed to do was apply our inverse operations and then go ahead and solve it again, just a quick little refresh. Inverse operations are performed. Proceed to solve. So, that’s what we did in the previous video.
Solve (x+2)^2-12=0
But we have a problem in this video because our equation from the previous video is not in the form that we have for this equation. As you can see, we actually have two XS, an X that is being squared, and a linear X. As a result, we can’t use the inverse operations. Right. I’ve already stated how that will not work. So, what are our options?
Solve x^2-2x-7=0
The main point I want you to remember is that this equation is in the form X squared plus ABX plus C equals zero. And the equation that was really simple to solve was something like X minus H. The sum of quantity squared plus K equals zero. Don’t be concerned about the positives or negatives, or the HK, B, or C. That is completely irrelevant at this point.
What I want you to understand is that the equation we’re having difficulty with is in this format. And this equation, which was simpler, is written in this format. And what is the real distinction? The main difference is that this is written as a squared binding. That is what gives us the squared singular X. If we wanted to go further, this is literally just an X minus H multiplied by an X minus H. I’d like you to pay close attention to what we receive. We’d get an X squared less two H squared plus a H squared. Right. Then it’s truly plus AK equals zero.
And the reason for doing so, as you can see, is that this is what we call a perfect square trinomial. Furthermore, all perfect square trinomials can be factored down to a binomial squared. So, what are we to do? What should we do if we have this equation in standard form and want to rewrite it as a perfect square trinomal?
So, what we can do is recognize the value H that will result in a perfect square trinomial. When I have a seven over here, this can get a little confusing. So what I’m going to do is add the seven to the other side. As a result, an X squared minus a two X equals a positive seven. And, once again, I’m trying to figure out what this H squared is that will result in this perfect square trinomile. Now, writing an HQ may be a little perplexing. So what I’m going to do is use the value C. So, once again, what I’m looking for is the value C that will result in this perfect square Trinomial. So now I want you to take a look at this relationship. And if I want to start with a negative two H and work my way up to this H square. That’s what I’m looking for. How, for example, can I replicate that? So, what I can do here is divide it by two and then square it. And when I do that, I get a H squared because it doesn’t matter whether the value is negative or positive. It will give me the H squared once it is squared.
So, if you look at this example, don’t be concerned about the X’s. We’re only concerned with the negative two coefficients in this case. So, if I want to find my value C, all I have to do is square my middle term, which is a negative two divided by two. Negative two divided by negative two equals negative one. Negative one squared will equal positive one. We could summarize this in your class as a B divided by two. B is the middle term quantity squared, which equals your C. That will equal the value that will result in our perfect square trinomile. So I get an X squared minus two when I do that. Seven is equal to X plus one. But keep in mind that whatever you do to one side of the equation, you must also do to the other side, right? We can’t just add a one to an equation and call it an equation. As a result, we must maintain balance. So what I’m going to do is add another one over here. I want you to notice this now. Isn’t this a perfect square trinomial? This is exactly what we were looking for in this format. So when I take my middle term divided by two and square, it will always find me the value C that I need to create my perfect square trinople. Now I just need to figure out how to factor this in. So, what is this value exactly? Returning to the expanded form, if this is X squared minus two H plus H squared, these are both of your H’s. In other words, the square root of whatever your C value is. As a result, H will be the square root of your C value. Then, if the middle term is negative, my two binomials will also be negative. If my middle term was positive, my two binomials would be positive as well.
Completing the Square
As a result, I can factor this now to an X minus one, and the quantity squared equals eight. And now I want you to see that this is in the same form as in the previous video, which is very simple to solve using our inverse operations. So, to solve this, I’m just going to take the square root of both sides and then add a one. Okay. And remember, when you’re taking square roots, I can break up eight into four times two. That’s how I arrived at two squared. Also, remember to include the plus or minus whenever you introduce the square root. I mentioned at the beginning of this video that we can still write this in factored form.
These will be the solutions, or the roots of the equations. But what if I want to examine the factored form? The only reason we want to factor is to use the zero product property, which makes life easier. However, if a problem is not true, then using this method of completing the square is exactly what we will need to do. But what if I want to know what that factor form is? You challenged me to factor this at the beginning of the video. What is the solution? So all I’m going to do is set each of these solutions to X and then set them to zero. Because if I provided the zero product property, each solution would be set to zero, and those solutions that are set to zero are the factors.
So there you have it, ladies and gentlemen, the factored form of this equation, which will be equal to an X squared minus two, an X minus seven, and an X minus one quantity squared minus eight. So either form will work, but hopefully you understand that when something like this is difficult to factor using this process of creating this perfect square by completing the square, we can use inverse operations to solve it. Is going to be very useful, and going to factor form was really not that bad, so factoring failed us, but that is okay. In the next video, I’d like to go over this process a little bit more and work through some more examples, even some of the more difficult ones, to help you solve any quadratic. Because with this technique, we can solve for any quadratic, whether it’s factorable or not.
Survive Math Class PDF | Facebook Community | Subscribe to my Channel
My Courses | Instagram