All right, guys, in this example, I want to cover some tips to help you with this word problem with bearings which usually confuses the heck out of students. So hopefully, some of the tips that I’m going to cover in this video will help you understand how to solve a word problem and give you a better understanding of how to use and solve for bearings.
Part One: The Problem
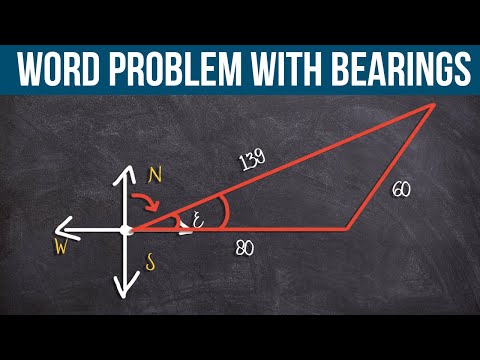
So in this example, we have a ship that travels 80 miles east from Port. Now, I’m just going to stop. Right. Because one of the first things that we always want to do when we have a word problem is to draw a picture. And you’ve probably heard from your teacher before. When you’re doing word problems, draw a picture, draw a picture, draw a picture. Right. The reason why that’s so helpful is it allows us to visualize what exactly is happening because otherwise, you’re just looking at these words, and it’s like blah. Right. So our primary goal is extracting a picture, extracting mathematical equations that we can then go ahead and understand and solve for it. So I have a ship that travels 80 miles to ease. So whenever I have this kind of, like, bearing and direction, the first thing we’re going to do is create a Cardinal direction.
Then from there, what you’re going to do is you’re going to have the north right, east, south, and west. Now we have this point here. We’re going to call that go ahead and P for our Port. Now, it says the ship travels 80 miles to the east. So I need to go ahead and represent that somehow. So what I’m going to do is go ahead and draw a nice little line going out here. And then we can go ahead and end and let’s go ahead and label that to 80 miles. We’ll leave the units off for a moment.
Then it says it takes a turn in the northeast direction. Now, the northeast is very vague. We don’t know where it’s going. We know it’s in this direction. Somewhere over in here, it says you’re going to go in that direction for another 60 miles. So again, we have this northeast direction. So whenever I have this, I need to go ahead and create another Cardinal direction. So again, from this turning point here, I will go ahead and do exactly everything over. Again, I’m going to do north, and I’m just going to label this east, south, and west. Now, again, everything doesn’t need to look perfect. And everything else, hopefully, you’re getting the idea. Now we’re going in this direction. We’re going 60 miles. So again, I’m just going to go ahead and represent this with another line here. And nothing has to be perfect. Ladies and gentlemen, let’s go ahead and say here are going to be 60 miles. And then it says if the boat is now 130 miles away from Port. So now I’m going to connect the Port to where this boat is here. And I’m going to say that that distance is 139 miles.
Now it’s asking us what is the bearing from Port to the ship and what is the bearing from the ship back to Port? So here’s where the ship is currently. Here’s where its Port is, right. It traveled 80 miles to the east, then took a turn right out to this direction. When we’re looking for the bearing, what we’re looking for is we’re looking for an angle from due north. So there are a couple of different ways we can write bearings.
We’re looking for this angle, and we have a problem here because we don’t have a way to solve this angle outside of the triangle. However, hopefully, you’ll recognize here I have an oblique triangle and this oblique triangle. I have all three side lengths. Therefore, we have a way to solve this triangle, which is going to be using the law of cosines. Another tip that I like to kind of recommendations to my students. When you’re looking at a problem like this, there’s already a lot going on. If you look at the words, sometimes it’s like mental overload. Now you create a picture to represent and extract some of the information. Now it’s also a kind of cognitive overload. I know what I need to do. I need to find the angle right here inside this triangle.
So to go ahead and do that, what I’m simply going to do is I’m going to redraw this one more time. Still, I’m just going to focus on this mathematically, and I’m going to rewrite them using A, B, and C because that’s how I like to solve my oblique triangles. So what I’m going to do is I’m just going to redraw the triangle. And again, it can look very similar to the one I just did. But forgetting about the Port and the ship and all that kind of stuff, I’m just going to label my oblique triangle the way I like to label all my oblique triangles, just like this. Remember, we have our opposing side lengths. A this is going to be B, and this is going to be C. From this information, if we need to go ahead and solve for A, I know I can use the law of cosine here.
So hopefully, you either have this memorized, or it’s on the board, or your teacher gives you a formula sheet that you can go ahead and reference. Okay. Now, it doesn’t matter what angles we’re dealing with. We can all interchange them. A, B, and C. This will be your typical formula for the law of cosines when we want to solve for an angle. Now, the cool thing is we know what B is. That’s going to be 80. We know what A is. That’s 60. And we know C, which is 139. So now, I’m going to go ahead and plug them into my formula. Okay. And now, to go ahead and get to this next point, I’m going to want to use my calculator. Right. So remember, when I want to solve for my angle A, we’re not solving for the cosine of A; we’re solving for the angle of A. So make sure that you undo the cosine by now. Go ahead and type in the cosine inverse of all this information. Okay. And now I’m just going to plug this into my calculator. Just make sure you’re careful when plugging it in, and then make sure you also take the cosine inverse. So, therefore, we can find our angle A.
So now you can see that A is equal to five-point 92 degrees, which is a pretty slight angle. And if you look at this triangle, like initially how I had it, that can make some sense. And again, that’s important about drawing your angles because, if this angle is like obtuse or something, you say something seems off. So that’s why it’s always nice to have a general picture of your triangle from the original problem. So you can make sense of if your answer is correct. Remember, that’s the angle right here. We’re looking for this angle. So the nice thing is, remember, these two angles will be complementary. So these angles are going to be complementary.
So all I need to do to find this angle is subtract this angle from 180 degrees. And again, this is the rounded version of the angle. But again, inside my calculator, I’m going to use the exact answer, and therefore, I get a rise of 84.07 degrees. When I want to go and answer this question, I’ll say the bearing from Port to the ship is 84.07 degrees. Or another way, we could say that it will be north 84.07 degrees east. So that’s just another way we could do bearings.
Part Two: The Problem
The next question we have here is finding the bearing from where the ship is back to Port.
So you can think about the first answer: let’s say you have station control at Port, right? They’re trying to see the bearing from the Port to the ship. Let’s say they needed to go ahead and find them. That’s why that would be important. Now, the other answer is from the ship to the Port. Let’s say they need to return to Port. And what direction do they need to turn? So, to find that answer, we need to create another Cardinal direction. So what I want you to recognize here is if this is going to be my due North Mrs. East southwest, again, my bearings will go from due north. So what I need to do is find the angle from here. Now that’s going to be very difficult to go ahead and do because how do I feel to see this angle? The only thing I can figure out is how to find this angle. And what you could do is also extend this line right here. And if you think about parallel lines in the transversal, remember we have those angle relationships, corresponding angles, and alternate interior angles.
So the one thing I want you to recognize here is that angle and that angle is going to be equal to each other. So, therefore, if I can find this angle and that angle, I’m going to be able to cover that side, and then I need to add 90 degrees. The nice thing about having a triangle is I only need to figure out one more angle here to go ahead and add these two to find my missing third side. So going back to my triangle, now I’m going to want to go ahead and find this angle C and then go ahead and find my angle B. But again, I can subtract those two from there. Now it’s very important to make sure that you stored answer A, so, therefore, you have that in your calculator because, again, remember, we’re going to want to subtract that from 180.
Now, we will write the law of cosines to find angle C. So remember, A will be 60, B is equal to 80, and C equals 139. Again, remember we’re trying to solve for C. Therefore, I will take the cosine inverse to undo the cosine. So I’m going to plug this all into my calculator that C equals the cosine inverse. Okay, when I do that, I get 166.15, which will be seen. And again, I’m going to store this because we already had A, which I wanted to store. And now what we need to be able to find is going to be B. So again, remember if I have two angles of a triangle, I can subtract those from 180 to find my missing angle. So B will be 180 degrees minus the stored answer for A, minus the stored answer for C.
When I do that again using my calculator and storing this, I’m going to go and have 7.92 degrees. Again, that is going to be my answer B. Now again, we have to remember what all this context means. Why is this again helping me find my bearing? So what I want to do is go back to the original picture so we can go and take a look.
So again, remember what we found? We found this angle C because of alternate interior angles; this line is parallel. They both intersect with this line. So C is going to be equivalent to this angle as well. From here, that’s going to be from this red line to the X-axis. Then we also just found B, which will be this angle as well. So if I add B plus C plus 90 degrees, that’s going to give me the bearing from due north over to this angle because you’re figuring a ship at this point, and you need to find the bearing back to the Port we’re going to go from due north all the way around to this line which is going to take you back to Port. So, therefore, I’m just going to take my angle B plus my angle C, and I’m going to add 90 degrees. That is going to give me my bearing. So when I do that, I get 264.7 degrees. Now again, let’s go ahead and check our work. Because again, remember we created this original graph here, so if I was to go ahead and grab this from due north 264 degrees. Well, from here to here is 90. From here to here is 180, and from here to here is 270. So 264 will be just a little bit shorter, right? So it’s going to look something like that probably. Does that look like the angle I need to go from the ship back to the Port? Yeah, not too bad, right? You can see I’m in the right frame. It’s not perfect. My drawing is not pictured but again, and you can see that this angle, this bearing here, is roughly a pretty good match going back to my Port. Okay, so now I need to finalize again. The answer did a lot of work, so we’re going to say the bearing from the ship to Port is 260. 64.7 degrees.
So, there you go, ladies and gentlemen. Hopefully, this was helpful for you and some of the tips that I have for you along the way. If you want more examples, check out the playlist and resources I have for you below, or check out the following video.