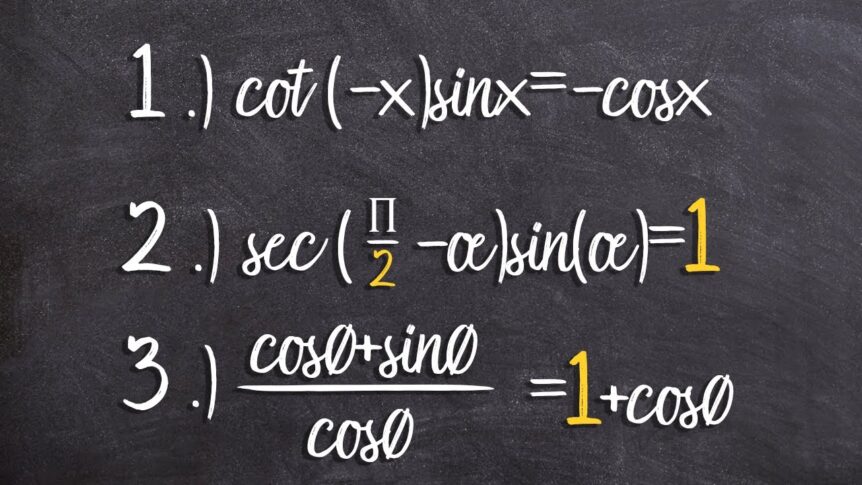Today, I want to verify some basic trigonometric identities. Trigonometric identities can become very confusing quickly, so I like to go over some basic identities to get an idea of what we’re trying to achieve and how we can approach each problem. What you do for one problem might work for another, making verifying trigonometric identities tough. It’s important to practice as many examples as possible and practice basic identities to see the relationship between identities and algebraic operations.
Example #1: cot(-x)sinx = -cosx
When verifying identity, we want to make one side look like the other side. I usually pick the most complicated side. In this case, I have two functions being multiplied on the left, whereas I only have one on the right. It will be much easier to simplify these two functions down to one rather than take cosine and rewrite it as cot(-x)sinx. I want to think about one side at a time and focus on how I can simplify the left side. One of the first things I recognize is the -x. Think about even/odd identities whenever you see a trigonometric function of a negative variable. These identities are very important to have a good grasp on.
The cotangent of -x is equal to -cotx, which we’ll multiply by sinx. Since I’m not working with a negative x, I’m not going to use parentheses here anymore. We can also think about this as -1⋅cotx⋅sinx. Now, we need to think about simplifying the left-hand side, so it’s just a cosine. The most common way to do this is called the division property: If 3/3 = 1 and (x+3)/(x+3) = 1, what will cos(3)/cos(3) equal? Also 1. Whenever you have the same term, expression, or function of the same argument in the numerator and denominator, you can divide them out.
That only works when terms are separated by multiplication, but this is a simple example. I need to know what identities I can use to rewrite my cotangent and sine, so I’ll have some numerators and denominators. Many of my students get stuck here when they first learn trigonometric identities because they don’t know which ones to choose. There are three different ways to write cotangent and sine using a fraction.
Quotient Identity: cotx = cosx/sinx Reciprocal Identity: cotx = 1/tanx Reciprocal Identity: sinx = 1/cosx
We need to decide how to rewrite one or both of the expressions. Something will divide out, but I’ll be left with just a cosine. I already got the negative that I wanted. Now, I need to figure out how I can have something divided out, so I’m just left with the cosine. Using cotx = cosx/sinx will put a sinx in my denominator, which will divide out with the sinx in the expression because you could rewrite it in the numerator. I’ll rewrite the cotx as cosx/sinx.
You don’t need to keep the 1, but I want to make sure you understand that when I rewrite this as a sinx in the denominator & cosx in the numerator, the other sinx is really over 1. Since my terms are separated by multiplication, and I have the same function in the numerator in the denominator, they will divide out. I now have -1⋅cosx/1, which equals -cosx, now equal to the right-hand side.
Example #2: sec(π/2 – α)sin(α) = 1
In this example, we have trigonometry functions on one side and a number on the other, so we want to work on the left side again and see how we can simplify these down into a number. Whenever something is divided by itself, it equals 1. If I want to get to one, I need something to be divided by itself. Unfortunately, it does not look like anything is being divided by itself in this problem. It looks pretty confusing. Many students will see π/2 – α and automatically get confused because it’s an expression inside the argument. When you see a negative argument inside of a trigonometric, remember it’s a cofunction identity. Cofunction identities are very important to recognize.
The first thing I’ll do is rewrite this with my cofunction identity. The secant of π/2 – α is equal to the cosecant of α. Cosecant and sine are reciprocal of each other. The product of a reciprocal times a reciprocal, such as 3/4 x 4/3 = 12/12, which equals 1. Maybe it’s not apparent that these are reciprocal, so let’s go back to our reciprocal identities.
cscα = 1/sinα sinα = 1/cscα
Students often make the mistake of applying both identities to both functions. Our goal is to be able to divide something by itself, so I don’t want to rewrite csc(α) as a 1/sinα and sinα as a 1/csc(α). There’s nothing mathematically wrong with it but it’s not what we want to do. I’m going to take csc(α) and rewrite it as 1/sin(α). We’ll have 1/sin(α) ⋅ sin(α)/1. These will divide out into 1, leaving us with a 1/1 = 1.
Example #3: (cosθ + sinθ) / cosθ = 1 + tanθ
My last trigonometric identity example is much more confusing. We have addition and division rather than just multiplication, and there aren’t any identities like the cofunction or even odd/identities that we can apply. We need to rely on algebraic operations. As we’ve been dividing things out to get 1, some students will get tripped up by the cosθ/cosθ, but we have to rely on trigonometric operations. Even though this is division, the identity I want to look into is the distributed property. If I have a ⋅ (b+c), it’s important to remember that a will distribute to both b and c inside of the parentheses, leaving me with ab + ac. The same thing works for division. If I have (b + c)/a, a gets divided into the b and the c.
Another way to look at this is with fractions: let’s say 1/5 + 3/5. As long as the denominator is the same, you just add the numerators. 1+3 = 4, in this case, the answer is 4/5. In this example, I can go to the right and simplify or actually separate it out. I can write (1+3)/5 as 1/5 + 3/5. Both of the terms in the numerator got divided by 5. You can look at it algebraically or you can look at it with an example. Students often divide out the cosines and are left with 1 + sinθ, which is not an identity. While some of the logic is correct, algebraically, they’re not dividing the cosine properly.
Instead, we want to rewrite this with the cosine divided into both terms of the numerator. Hopefully, you recognize that whenever I have a trigonometric function over a trigonometric function that is exactly the same, it equals 1. Sinθ/cosθ = tanθ, now equal to the right-hand side.
I hope this was helpful. If you want more examples of verifying trigonometric identities, check out the examples and resources below.
Facebook | Instagram | Twitter | LinkedIn | YouTube | Udemy