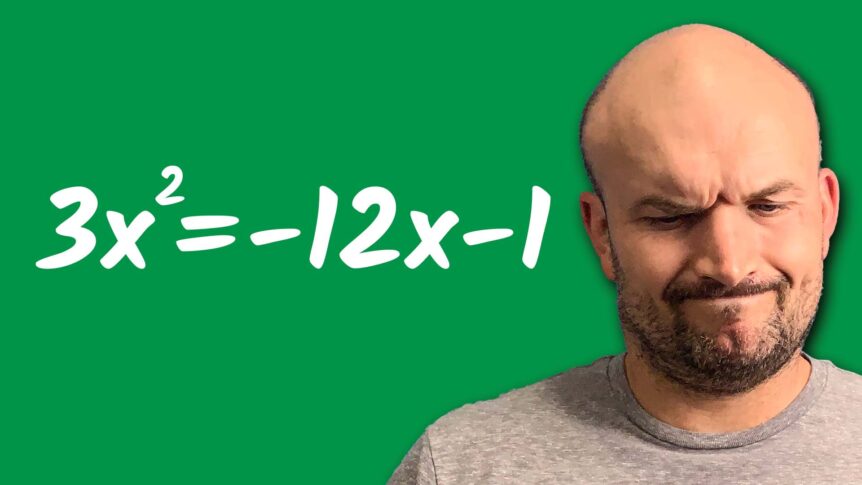Easy VS Hard
Now, this is a hard example, and this is a hard example because it doesn’t look like the easy one. We can’t apply our inverse operations. We can’t just isolate or undo the operations happening to our X because we have more than one of them. So we have a couple of options. We could look into factoring. And when we factor, what we want to do is set them into two factors that are equal to zero. The problem with this is under real rational numbers. I’m not aware of any two numbers that multiply to give me a negative four and add a positive two. It would be cool if I could use the same operation I did for the easy problem on this problem. Let me think, is that possible? Yes, indeed, it is possible. We have been working on the process through the series of posts called “Completing the Square.” Because what I want you to recognize here is why these are different is that this is written as a binomial square.
This is an expanded form.
So what we want to do is create that perfect square trinomal. Because this is not a perfect square trinomial. So the first thing I’d recommend doing to solve this by completing the square is to go ahead and add a four to the other side.
Therefore, what will leave us with is an X squared plus two. X is equal to a four. Now, this will be a value that I’m going to want to create my perfect square trinomal. And if you remember, in the last post, what we talked about was finding that value C. So remember, if we just wanted to find a value C that will create that perfect square, I can do that on the left-hand side and make sure you add the C to the right-hand side. Now, we need to figure out what C is? Well, remember, C equals B divided by two. Quantity squared, and B, in this cas,, willo. So two divided by two. Quantity squared is two divided by two is one. One squared is going to be a one. So therefore I have AX squared plus a two. X plus one equals a four plus one.
Now I want you guys to recognize I have created a perfect square trinomial that I can go ahead and rewrite as a binomial squared is going to equal five.
Now when I use my inverse operations, guess what answer I’m going to get the exact same answer I got in the easy equation.
So sometimes you’re going to get hard problems, problems that are not factorable. But it’s okay, you can go from a hard problem to an easy problem just by completing the square.
But I do have to warn you, not all problems completing the square are going to be easy. So for the rest of this post, what I want to cover is four different problems where completing the square can get hard. This is basically when students have a general understanding of completing the square like I’ve talked about in the previous posts. But start making mistakes. So let’s just go and take a look at four different examples and work through solving them.
Example #1
This first example actually isn’t that bad, but again, it’s just a good brush up.
If you understood what I talked about here in the first part of this post, then go ahead and try to do this problem on your own and then see if it’s going to match up with mine.
Remember, the main thing we want to do here is to create that perfect square on the left-hand side. So I’m just going to use a value C to represent that perfect square, and I’m going to add that C to both sides. Then define my C. Again, I’m just going to take C as equal to AB divided by two coins squared, which in this case it’s going to be a negative eight over two coins squared. Now you can use eight or negative eight. It doesn’t really matter. It’s all good, whichever one you choose. And therefore it’s going to be negative four. And because you’re going to square it, negative four squared is going to equal a 16.
Now what I’m going to do is I’m just going to add that to both sides so that’s going to be A plus 16 equals a ten plus 16. Now what I want you to do is recognize that this is going to be a perfect square trinomial right. Now, again, hopefully, you recognize what that is factoring, but a lot of students struggle with how to identify the form of the X minus a quantity square. Now again, remember, if my middle term in my quadratic is negative, then my middle term in my binomial is also going to be negative.
But remember, we do have a formula for how to find A. A is just simply B divided by two. So if I want to be able to find my A, I just need to say, well, what was my B divided by two? Well, that was negative eight divided by two, which is a negative four. So this is just going to be an X minus four quantities squared. And again, remember, it’s either could be plus or minus in this case. And then again, you want to look at the middle term of your trinomial. If that’s negative, that’s negative and that’s positive, then that’s positive. So X minus 420 squared is equal to a 26. And now I can just use my inverse operations. Take the square to both sides and I get ax minus four is equal to square to 26, which I don’t think I can simplify at all. Just make sure you include the plus or minus and then I’ll add affordable sides. And therefore X is equal to a four-plus or minus the square root of 26.
Just real quick, as we’re dealing with an easy problem, I’m not going to do this for the rest of the problems. But again, remember, if you were to try to factor this, that would not have worked, right. If you would have set this equal to zero and tried to factor it, you could have done that. Because what two numbers multiply to give you a negative ten and add to give you a negative eight. Right? Well, the closest thing we have is a negative ten and a positive one. Which would give you a negative nine. But we need a negative eight, so it’s not going to work factorable. You could find the factored form by setting them both equal to X. So we’ll just go ahead and separate them. So four plus the square root of six, and then X equals a four minus the square root of six, and then set them equal to zero, which is going to represent their factored form. So if I subtract these to get them all onto the same side, I’m sorry, that’s a 26 equals zero, and then this would be X minus four plus a square root of 26 equals zero, then that would be my factored form.
So I’m going to write it out here as an X minus four minus a square root of 26 times an X minus four plus a square root of 26. And you can see it has that being as the factored form, that would be very difficult to try to factor that in your head. I think you would agree. So that’s why using this completing square is so helpful. But if you need to find that factored form, you can always work your way backward by completing the square.
Example #2
Now let’s look at a problem that starts to get a little confusing. And the reason why this one gets a little confusing is that if you want to try to find C and you take your B divided by two quantities squared, well, you’re going to have a fraction, which is okay, that’s okay to have fractions. But again, it still confuses some students. So, therefore, that’s why I want to work through this one step by step. So anyway, five squared is going to be a 25 over four.
But again, let’s kind of like back up a second and just say what would really be the first thing I’d want to do in this problem? Now the last problem, I only had my variables on the left-hand side and I constantly right. So you can easily subtract the three to the other side. But if you’re okay with just keeping everything to one side, you can always do it at the end as well. And what I mean by that is rather than adding a C to both sides, you can also add and subtract the C on the same side. So for instance, what I mean by that is I could rewrite this as an X squared plus five. X plus C.
🗂️ Organized playlists by classes here🗂️
I need to create my perfect square trinomial. Now you could subtract that three. Or you can just leave it here and just say, well if I’m going to add a C I need to go ahead and subtract a C equal to zero. It’s the same thing as just putting the C and the positive three on the right-hand side. Now again, we figured out C was a 25 over four. So therefore I’m going to replace my C with a 25 over four.
I like to keep them on the same side when we’re using our vertex form. Now I’ll go ahead and add them over to the other side once I simplify them. But the first thing I recognize here is I actually want to simplify this. I want to take the three -25 or four. Well, the only way I can do that is if my denominators are exactly the same and in this case, they’re not. So to obtain common denominators, I need to multiply by a four over four. Now the next thing I can do to simplify this is I can factor this down to a binomial squared. Now again, we have to be able to recognize what is my A. Remember, A is B divided by two. So what was my B divided by two?
C is going to be five over two, right? You can be divided by two is five over two. So therefore I can rewrite this in factored form as an X plus a five over two quantity squared. Now this is going to be plus a twelve over four, right? That’s equal to three minus a 25 over four equals zero. So, therefore, let’s just go ahead and rewrite that. So that’s going to be a five-two quantity squared. Now twelve -25 is going to be a negative 13 over four is equal to zero. So you can see if you would have added everything to the right-hand side, it would have been already over there. But now I just need to do a couple of extra steps to go ahead and solve it.
So now what I’ll do is I’ll add a 13 over four to the other side. Then go ahead and take the square root and subtract a five half.
All right. There you go. Ladies and gentlemen, that’s going to be the solution to this quadratic.
Example #3
Now, another type of problem that can get students really messed up is when we have a number in front of our quadratic, completing the square only works when A is equal to one. And in this case, A is not equal to one, A is equal to three. So the first thing I’m going to do is I’m actually just going to divide everything by three. Now, again, that’s going to create a fraction over here. But that’s okay because again, our main thing, our main idea is creating that perfect square trinomal, and we have to have A equal to one to go ahead and do that. So when I divide everything by three, I’m not going to be left with an X squared equal to a negative four X minus a one-third.
Now, again, I’m going to leave the negative one-third over there. Remember, to create that perfect square trinomial on the left-hand side, I just need to add this four X. So now I have an X squared plus a four. X is equal to a negative one-third. Now, again, I’m going to be adding things on the left and right-hand side. But to determine that value, remember, we got to think, what is that value that I’m going to add? It’s going to be C. So X squared plus a four X plus C is equal to a negative one-third plus C. Don’t forget to add C to both sides. Whatever you do on one side, you have to be able to do on the other side. Now we just need to be able to figure out again what C is. C is opposite to B. Just B divided by two squared. It doesn’t matter if it’s positive or negative, right, because it gets squared. So in this case, I have four divided by two squared. Well, four divided by two is two. Two squared is equal to a four. So, therefore, I have an X squared plus a four. X plus four is equal to a negative one, three plus four.
Now, again, I can’t add these fractions unless they have the common denominator. So I’ll put that over one and then I’ll multiply by a three over three. Now, hopefully, you recognize I can simplify this. And remember when we’re trying to find A that’s just going to equal to my B divided by two. And remember, that’s going to be X plus A quantity squared. The reason why it’s plus is because my trinomal is going to be A-plus.
🙋♂️Have questions? Ask here🙋♂️
So what was my B divided by two? Well, four divided by two is just two. So, therefore, I can rewrite this as an X plus two quantities squared. Now here I have denominators that are the same. So four times three is 12, 12 plus a negative one is going to be a positive eleven over three.
Now I’ll just take the square root of both sides. Make sure you take the plus or minus when you take the square root to both sides. So now what I have is an X plus two is equal to a plus or minus the square root of eleven over three. Now I can’t really simplify that you could rationalize the denominator, I guess if you really want to, but in this case, then we’ll just subtract the two. So I have a final answer of a negative two plus or minus. Let’s multiply by the square root of three over three, I can distribute that three inside of the other radicals. That’s going to be a positive 33 divided by three. There you go, Lincoln. That is the solution to that equation.
So just remember this problem whenever you have a number in front of your quadratic and you’re trying to complete the square, then just go ahead and divide everything out by that coefficient to eliminate it.
Example #4
Now in this example, we could divide everything by two. But I actually want to give you again another technique that I like to use for the graph when I’m graphing using vertex form that you can also use for solving. Now in this case what I’m simply going to do though first is I am going to add the 20 to the other side and therefore I’ll have a two X plus a seven. X is equal to a 20.
Now rather than go ahead and divide everything by two, which you could definitely go ahead and do, there’s not a problem with that. What I’m going to simply do is actually plan on factoring out the two on the left-hand side. When I factor out the two, that’s just like reverse multiplication. It’s basically dividing a two out of your two X squared and your seven X. So when I do that, what I’m going to tain here is a two times an X squared plus a seven half. X is equal to a 20. Again, I’m only doing this on the left-hand side. Now the reason why I did it over here is that if you were divided everything by two, you would have had a seven-half anyways. But the reason why I like to do it on this case is you can just kind of see we have our perfect square trinomial is now going to be inside the parentheses. So again, now I need to find that value C that completes the square. So therefore I’m going to add a C inside the parentheses and then also on the right-hand side. Now I want you to pay very special attention to something I did. I multiplied my C times two.
🎯Survive Math Class Checklist: Ten Steps to a Better Year🎯
Why did I do that? Well, when I added a C inside here on the left-hand side, it’s inside the parentheses, right via distributed property. Right. If you go back and check my work. If you multiply two times both of those two times X squared is two X squared. Two times the seven half, X is going to be a seven X, right. So when I add a C, that’s technically me adding two C on the left-hand side, and on the right-hand side, that’s going to be exactly the same case I’m adding a two C on the right-hand side. So you’ve got to make sure whatever you’re doing on one side you have to do on the other side. So now let’s go and find my C.
Now again, remember C is going to be a B divided by two squared. In this case, I have a seven half divided by two, and sometimes that gets confusing to it. So let’s go and do it on the side. So if I had seven half divided by two, well again divided by two is the same thing as multiplying by one half, right. Because that’s just going to go ahead and multiply to one. And again when you multiply by the reciprocal, that makes my denominator equal to one, which is good. So therefore that goes down to one, right.
And then here I have seven times one and two times two which is four. So therefore that’s going to be quantity squared is really just going to equal a four. I’m sorry, not a four, a seven four squared. So let’s go and fix that. So it’s going to be a seven-four quantity squared. So what I’m going to do that is going to be a seven squared over a four squared which is a 16. So that’d be a 49 over a 16.
Now that is going to be the value I’m going to add for my C on the left and the right-hand side. Now we need to be able to figure out what this binomial is. Now again my middle term is positive. So therefore I’m going to have ax plus a quantity squared. So remember, A is just equal to my B divided by two, right.
So what was my B divided by two? B divided by two equals a seven four. So therefore I can simplify this to a two-times X plus a seven-four quantity squared. Now in this case I can go ahead and simplify that. So I can simplify this to 20 plus. Let’s see, I can divide that two over 16. I can write that as a 49 over eight. So, therefore, now I can put this as a denominator over one, and therefore get a common denominator here I’ll take a multiply by eight on the top and the bottom and therefore that’s going to leave me with 160 over eight-plus 49 over eight, which I can just combine to 160 plus 49 all over eight. Just make sure not to get rid of this two. I could either divide by two on both sides or you could just multiply by one half. It’s the same operation here. So when I do that I now have an X plus seven forces. Quantity squared is equal to a 209 divided by a 16.
Now I can just take the square root of both sides. I’m not really sure if there’s anything I can simplify with 209 but I can take the square root of 16 which is going to be four so therefore I have an X plus a seven force is equal to a plus or minus the square root of 209 all over four and now you can see I can just subtract my seven force to both sides and I’ll probably rewrite that in front so, therefore, my final answer is X equals a negative seven force plus or minus a square root of 209 divided by four and pretty looks like a pretty crazy solution, right?
So you can see how completing the square was definitely hard but again looking back at that original problem is not something you want to factor in either because you’re not going to be able to get that factoring problem outside in your head. Now you can see that completing the square was pretty difficult in this case but even if you look back to the original problem factoring would have been really difficult as well, right? You would have had to try to factor to get the solution so factoring can be easy but factoring can quickly get out of hand to be difficult.
The same thing with completing the square can be easy but also you’ve recognized this problem did not look that complicated, right? I mean it was decent but the numbers weren’t crazy you can see completing the square got pretty difficult so maybe is there even a better way than we have solved this equation? And yes there is one more method that we can use to solve our quadratics. This last example would definitely have been the easiest for us to try. So in the next post, I’ll do is I will explore exactly this new method, how it is created, where it comes from, and how to apply it in solving quadratics. I’ll see you guys in the next post.